Euclidean rhythms have roots in ancient Greek geometry but took a brief detour in particle physics before entering the world of modern music creation. Part 1 in this two-part series explores how Euclidean rhythms work and how composers and producers can manipulate and layer them to generate groovy rhythmic material.
The Euclidean Algorithm
Euclid of Alexandria: Toga wearer, geometry beefcake, unwitting musical innovator.
The Ancient Greek mathematician Euclid of Alexandria was lived in the 3rd century B.C. and is regarded today as the father of modern geometry. His writings encapsulate everything that was known about geometry in the Ancient Greek world. Thanks to Euclid, we know how to find the area and volume of 2D and 3D objects, how the Pythagorean theorem works, and that there is most likely no largest prime number. The principles of Euclidean geometry have stood the test of time and exceptions to Euclidean postulates (non-Euclidean geometry) only began to be discovered and articulated in the nineteenth century.
In his most famous work, the Elements, Euclid demonstrated how higher-level theorems can be deduced logically from a handful of lower-level axioms. The veracity of each theorem is demonstrated by a proof (the bane of high school geometry students everywhere) that articulates the logical steps required to accurately create or describe the properties of increasingly complex geometric constructions. This logical, modular working method was significant to the development of the modern practice of mathematics. Each proof ends with the acronym Q.E.D. (quod erat demonstrandum, "it has been demonstrated").
The Euclidean algorithm is one of the most famous propositions in the Elements. It is a set of rules (or logical steps) used to find the greatest common divisor between two integers. In other words, it answers the question, "What is the largest number that divides both a and b evenly (without fractions or decimals)?" The algorithm is recursive, meaning that it repeated until a solution is found. The easiest way (for a non-mathematician like me anyway) to understand the Euclidean algorithm is to imagine it visually as a rectangle with one side of length a and the other of length b. Let's assume that a is the longer side and b is the shorter side.
To start the algorithm, take the largest perfect square that will fit within the rectangle — a square with all sides equal to b (blue in the diagram above). Place that square inside the rectangle so that it shares an edge with one of the two short edges of the rectangle. Now look at the portion of the rectangle not covered by the square (the pink area in the diagram). Can you fit another square (of the same size) inside this remaining area?
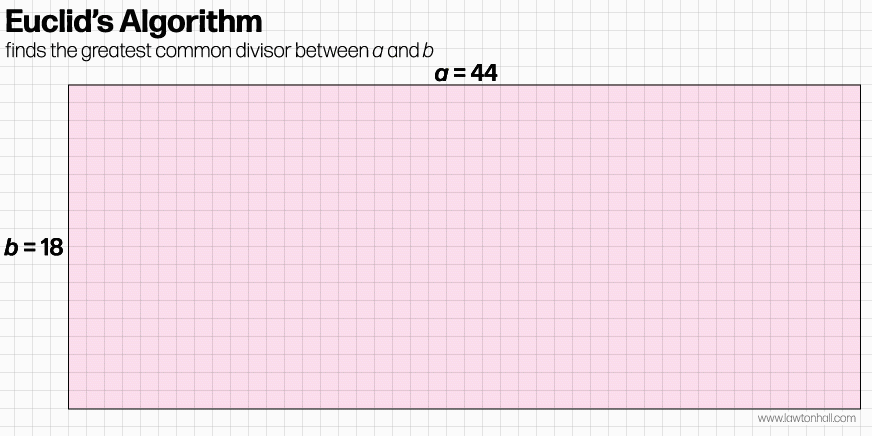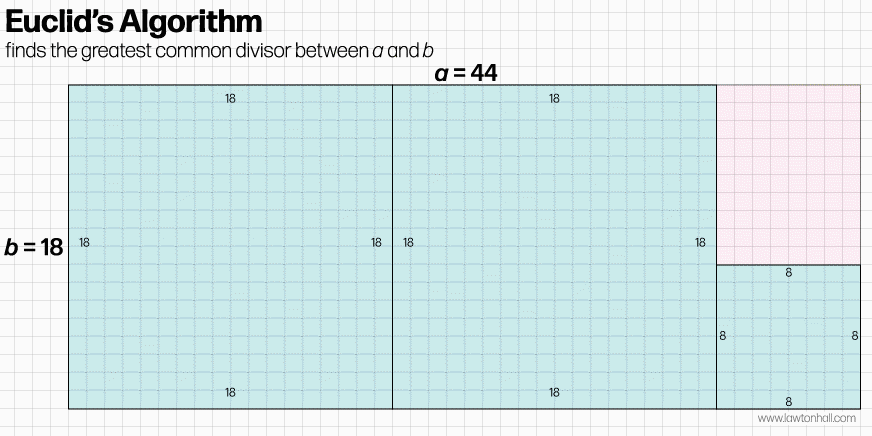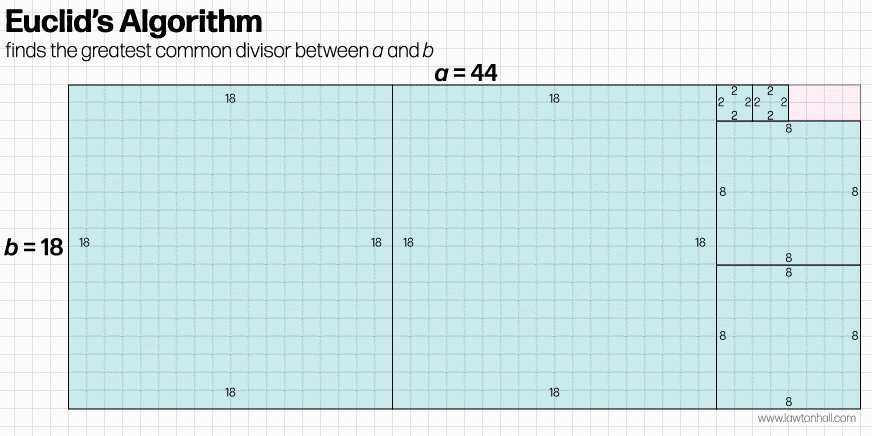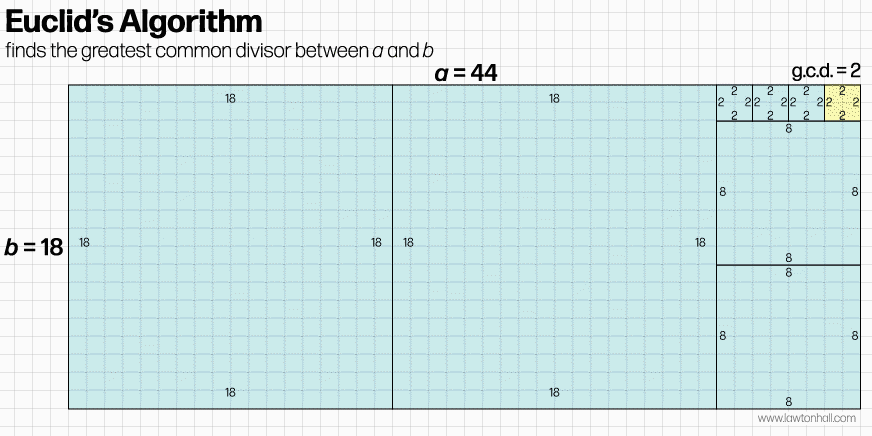
If you can fit in more squares of identical size, keep doing so until no more will fit inside the remaining rectangle. If at this point the squares cover all of the area of the original rectangle perfectly, the algorithm ends and b is the greatest common divisor between a and b. Easy right? If there is still space left over inside the original (pink) rectangle, start the algorithm over again by creating a new square with edges the length of the short edge of the remaining rectangle left over after subtracting the squares from round 1. Keep looping through this process (creating smaller and smaller squares each time) until the entire area of the original a * b rectangle is covered. The length of the edges of the smallest square is the greatest common divisor between a and b.
Cool. So what does this have to do with music?
It doesn't. At least not yet. In order to understand how Euclid's algorithm made its way into music, we first have to talk about nuclear physics (yes, really).
In 2003, Eric Bjorklund was working on a spallation neutron source (SNS) particle accelerator at Los Alamos National Laboratory. Please don't ask me to explain what a spallation neutron source particle accelerator is because I haven't the faintest idea. In order for this extremely precise and expensive (I assume) piece of equipment to work as intended, a gate needed to be opened a certain number of times within a certain window of time (for example, 7 times in ten seconds). It was important that the timing of the gates be spaced as evenly as possible within the window.
Spallation neutron source (SNS). I have no idea what this thing does.
In music, we would use a tuplet to show this even division of a duration—a 7 against 10 polyrhythm, perhaps. However, this gate was controlled by a pulse signal that only occurred at regular intervals (e.g. four times per second). The gate could only open when a pulse occurred which means that the fractional durations in our 7:10 tuplet wouldn't work. In musical terms, it is as though the 7:10 polyrhythm had to be quantized to a sixteenth-note grid.
Bjorklund's solution is an algorithm that takes a number of gate-openings (k) and the number of pulses within a given window (n) and finds the most even way to space gate-openings within the window using only integers so that they can be triggered by the pulse signal. (I will use the variables k and n throughout this post.) If n is not evenly divisible by k, there will be two different durations between gate-openings. Bjorklund's algorithm arranges the varying durations for maximal evenness. For example, k = 7 and n = 16 produces:
[ 1, 0, 0, 1, 0, 1, 0, 1, 0, 0, 1, 0, 1, 0, 1, 0 ]
Where 1s and 0s represent regular pulses and gate-openings occur on 1s only. We can write the time between gate-openings as durations (in pulses) like this:
[ 3, 2, 2, 3, 2, 2, 2 ]
Euclidean Rhythms in Music
Later in this post I'll show how Bjorklund's algorithm works, but first I want to discuss the musical applications of this discovery. In 2005, mathematician and McGill University professor Godfried Toussaint was a researcher at CIRMMT at the Schulich School of Music and published an article titled "The Euclidean Algorithm Generates Traditional Musical Rhythm." In it, Toussaint shows that Bjorklund's SNS algorithm is remarkably similar to Euclid's algorithm. Both are recursive and use the same basic process of subtracting regular-sized units from a larger whole, finding the remainder, and then repeating the process until there's nothing left to subtract. A mathematical proposition from before the invention of the windmill is related to problems in particle accelerators over two thousand years later.
More importantly, however, Toussaint found that if you re-imagine Bjorklund’s algorithm in musical terms, it can produce rhythms that are found in numerous and disparate styles of music from around the world and throughout history. Instead of dealing with pulses and gate-openings in a particle accelerator, he applied the algorithm to regular subdivisions (e.g. eighth or sixteenth notes) and notes that occur on those subdivisions. Bjorklund’s algorithm produced sequences of maximally even rhythms, which had been a source of fascination for Toussaint and other musicologist-mathematicians researching the music of sub-Saharan Africa.
Toussaint uses the notation [k, n] as a shorthand, which I will use throughout the rest of this post. k must always be lesser than or equal to n. He also diagrams the cycles using rhythm necklaces, a useful way of visualizing rhythmic loops.
The maximally-even quality of these so-called Euclidean rhythms strike a balance between regularity (they never stray too far from a regular beat) and syncopation. The most interesting Euclidean rhythms occur when n is not evenly divisible by k, such as our [7, 16] example above, which produces a [3, 2, 2, 3, 2, 2, 2] duration pattern:
These irregular Euclidean rhythms will always feature exactly two different note-lengths/durations (e.g. 3 and 2 for [7, 16]) that are always only one integer apart, which means that, despite their potential complexity, notes in a Euclidean rhythm will be either on the beat or off the beat (syncopated). The longer durations (3s) produce subtle agogic accents (accents of duration), but these don’t disrupt the overall forward momentum of the rhythm since they are only slightly longer than the shorter notes. This makes Euclidean rhythms prime material for looping grooves (a.k.a. ostinati, if you’re feeling fancy) that form the foundation for songs and dances.
Here are some examples of Euclidean rhythms in action:
Ewe drumming from Ghana features the [7, 12] Euclidean rhythm as a bell pattern played by the gankogui (agogô). This bell pattern is the backbone for all of the other drum parts:
The [4, 7] Euclidean rhythm can be heard throughout the Bulgarian ruchenitsa dance:
Dave Brubeck’s Blue Rondo à la Turk features a pervasive [4, 9] Euclidean rhythm that has similarities with “limping” Turkish and Balkan aksak rhythms:
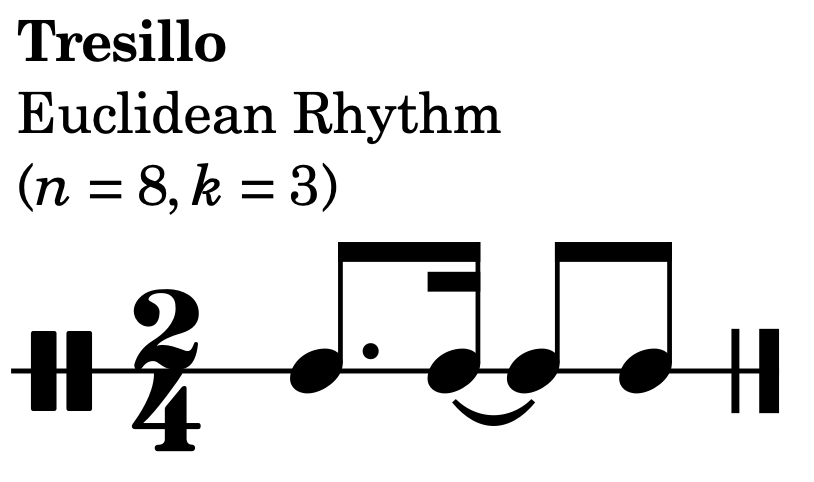
The Cuban tresillo rhythm (Euclid[3, 8]) is the foundation for the habanera, the tango, son matumo, mambo, reggaeton and numerous other Caribbean and South American dance forms. It enjoyed a moment in the spotlight throughout countless 2010s dance-pop hits (see also: Despacito):
Since the “discovery” of their algorithmic origins, Euclidean rhythms have been an inspiring tool for producers and composers (and the rest of this post deals with how to create your own Euclidean rhythm grooves), but Euclidean and Euclidean-like rhythms also appear in modern compositions that pre-date Toussant’s paper. Late in his life, Hungarian composer György Ligeti (1923-2006) became fascinated with the music of sub-Saharan Africa and built many pieces on the juxtaposition of rhythms inspired by Aka music from central Africa. S.A. Taylor, in his analysis of Ligeti’s later works, finds numerous maximally even rhythms (he does not use the term “Euclidean” but cites other musical research by Toussaint) throughout the violin and piano concerti and often used them as a kind of isorhythmic talea. Ligeti’s sketches show that he was directly inspired by Aka rhythms and often superimposed multiple metric streams to create his rhythmic palette, which can be heard in his 1993 violin concerto:
In Practice
I'm hesitant to read too much into the "world music rhythms" aspects of Toussaint's article. Every musical tradition approaches rhythm differently (sometimes wildly differently). Isolating accents or bell patterns between disparate musics to find mathematical similarities between them feels like an overly reductionist, Western-music-theory way of looking at things that disregards the cultural forces that influence musical expression. Individual musicians innovate and experiment with rhythm in every musical culture and are constantly producing music that defies labels and doesn't fall within convenient ethnomusicological taxonomies. Moreover, simple patterns like a four-on-the-floor disco beat are technically Euclidean rhythms (k = 4, n = 4), but who is going to argue that Donna Summer and Giorgio Moroder had ancient Greek geometry in mind when recording I Feel Love?
What is certain, however, is that the Euclid-Bjorklund algorithm is capable of producing rhythmic patterns that at the very least feel intuitive and familiar. They avoid some of the cold, artificial, made-in-a-lab sound that can result when generative or algorithmic composition techniques are employed non-critically. For this reason, Euclidean rhythms are an incredibly powerful and versatile technique for composers, producers, and beatmakers to add to their toolkit. A single Euclidean cell can form be used like a bell pattern, forming the basis for an entire piece. (The second movement of my drum set quartet Codex uses a [5, 12] Euclidean rhythm this way.) More complex grooves can be constructed by layering different Euclidean rhythms on top of one another, each with different k and n values and varying durations for the underlying pulse. This produces polyrhythmic textures that feature syncopation in each rhythmic stream:
Example #1 — Click to expand
Changing k and n in just one of the rhythms produces a different texture:
Example #2 — Click to expand.
This technique isn’t limited to percussive/rhythmic material. By assigning pitches to the same layered Euclidean rhythm, it’s possible to create a hypnotizing, groovy minimalist texture:
Example #2b — Pitch instead of percussive sounds. Click to expand.
If n is much larger than k, the resulting Euclidean rhythm will be sparse, with more time between notes. As k approaches n, more pulses get filled in, and the texture becomes more dense. (When k = n, all pulses are filled with notes). This allows a beatmaker to create rhythmic contrast between different sections of a song or composition, by manipulating the event density through the relationship between k and n values in a Euclidean rhythm stream.
Ex. 3 – Changing k value to increase event density. (Click to expand)
Do It Yourself
There are several software options (many free) that allow you to start experimenting with layering Euclidean rhythms. User dbkaplun created a free rudimentary browser-based Euclidean rhythm generator available on GitHub. Polyrhythmus is a module built by Benniy C. Bascom for the Max/MSP platform. Imogen Heap's Box of Tricks is a Kontakt instrument built upon Euclidean rhythms. There are also numerous apps. I personally use the free Bjorklund quark for SuperCollider by Fredrik Olofsson. I especially appreciate the PBjorklund functions that work within SuperCollider's pattern library. I have included SuperCollider code at the bottom of this post (after the references) to help you get up and running with the Bjorklund quark.
As always, you don't need software to start using this technique, though it helps to be able to quickly try out and tweak different parameters to find patterns that you like without spending too much time on the algorithmic side of things. If you have a Euclidean rhythm platform that you're happy with and want to explore ways of using them to structure longer, dynamic musical passages, check out Part 2 of this post, where I explore techniques that aren’t strictly loop-based and evolve over time.
If you're working out Euclidean rhythms by hand or developing your own system, it's time to look under the hood of the Bjorklund algorithm. Start with an array (list) of n zeros and ones representing pulses. The first k pulses are ones and the remaining pulses are zeros. The order of the zeros and ones will change as you work through the algorithm, but there will always be the same number of zeros and ones. For n = 13 and k = 5, this is the starting array:
[ 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0]
Next, move each of the last k zeros and append them to the ones to create k [10] sequences:
[ [10], [10], [10], [10], [10], [10], 0, 0, 0 ]
The goal is to get as many of the sub-sequencies (e.g. [10]) to be the same. After this first step, the zeros left over at the end are the remainder (italicized). Move the three remainder zeros to the end of the first three [10]s, like this:
[ [100], [100], [100], [10], [10] ]
Repeat the process of moving sequences at the end of the list by appending them to elements at the front. This time the [10]s are the remainder, and get appended to the first two [100s]:
[ [10010], [10010], [100] ]
The algorithm ends when there is only one (or no) remainder. Since there is only one [100] remainder sequence, this example is complete. You can flatten (remove the brackets) from the array to better visualize the rhythm:
[ 1, 0, 0, 1, 0, 1, 0, 0, 1, 0, 1, 0, 0 ]
To convert this array of pulses to durations, simply count the number of pulses between each 1:
[ 3, 2, 3, 2, 3 ]
The sum of the durations should equal n. Once this process is complete, you can produce variations on the same Euclidean rhythm by rotating (shifting the durations left or right) the duration array. Since the Euclidean rhythms are meant to cyclical, it is possible to start at any point in the loop and it will still produce a rhythm that is maximally evenly-spaced. There are k-1 possible rotations, but some rotations may be identical:
[ 3, 2, 3, 2, 3 ] → [ 2, 3, 2, 3, 3 ] → [ 3, 2, 3, 3, 2 ] → [ 2, 3, 3, 2, 3 ]
(Interesting musical results can happen when two rotations of the same Euclidean rhythm are superimposed on one another). To map these numbers to musical terms, choose a duration for the length of each underlying pulse. Sixteenth notes or eighth notes are common but any duration is possible. Each duration integer is simply a multiple of the underlying pulse. E.g. 3 eighth notes = dotted quarter note; 2 eighth notes = quarter note, etc.
Conclusion
The centuries-long journey that the Euclidean algorithm took from geometry to music demonstrates the value of looking for musical inspiration in unexpected places and across disciplines. Godfried Toussaint’s paper includes many more examples of Euclidean rhythms in practice and it’s worth doing some Googling to listen to examples of how they have appeared in various musical contexts.
This post should give you the background and theory needed to add Euclidean rhythms to your composition/production toolkit. As with any generative music technique, it’s best to keep an open mind and not get too hung up on the purity of the process itself. Follow your ears, your heart, and your gut (not necessarily in that order.) Post your experiments with Euclidean rhythms here in the comments or tweet them to me @_greathorned.
With a little creativity, Euclidean rhythms can be used for much more than just beats and loops. Next week in Part 2 of this post I will show how the k and n variables in Euclidean rhythms can be treated dynamically to generate rhythmic streams that evolve over time. Until then—quod erat demonstrandum.
References
Bjorklund, E.. “The Theory of Rep-Rate Pattern Generation in the SNS Timing System.” (2004).
Nice Fracile, “The “Aksak” rhythm, a Distinctive Feature of the Balkan Folklore.” Studia Musicologica Academiae Scientiarum Hungaricae 44, No. 1-2 (2003), pp. 197-210.
Adam Harper, “How a Traditional Rhythm is Shaping Today’s Most Exciting New Music.” Fader (June 10, 2015).
Kwaku Ladzekpo, The Clave Matrix; Afro-Cuban Rhythm: Its Principles and African Origins (1997).
Ben Lynn, “Euclid’s Algorithm.”
Luke Mastin “Euclid of Alexandria — The Father of Modern Geometry.” The Story of Mathematics.
Godfried Toussaint, "The Euclidean Algorithm Generates Traditional Musical Rhythms." Proceedings of BRIDGES: Mathematical Connections in Art, Music and Science, Banff, Alberta, Canada, (July 31-August 3, 2005), pp. 47-56.
Steven Andrew Taylor, “Hemiola, Maximal Evenness, and Metric Ambiguity in Late Ligeti.” Contemporary Music Review 31, No. 2-3 (April-June 2012), pp. 203-220.